你知唔知, że… ?
W szkicu 2D jak i 3D istnieje wiele relacji, niektóre z nich są identyczne w obu przypadkach. Ale są pewne relacje specyficzne dla szkicu płaskiego i szkicu trójwymiarowego.
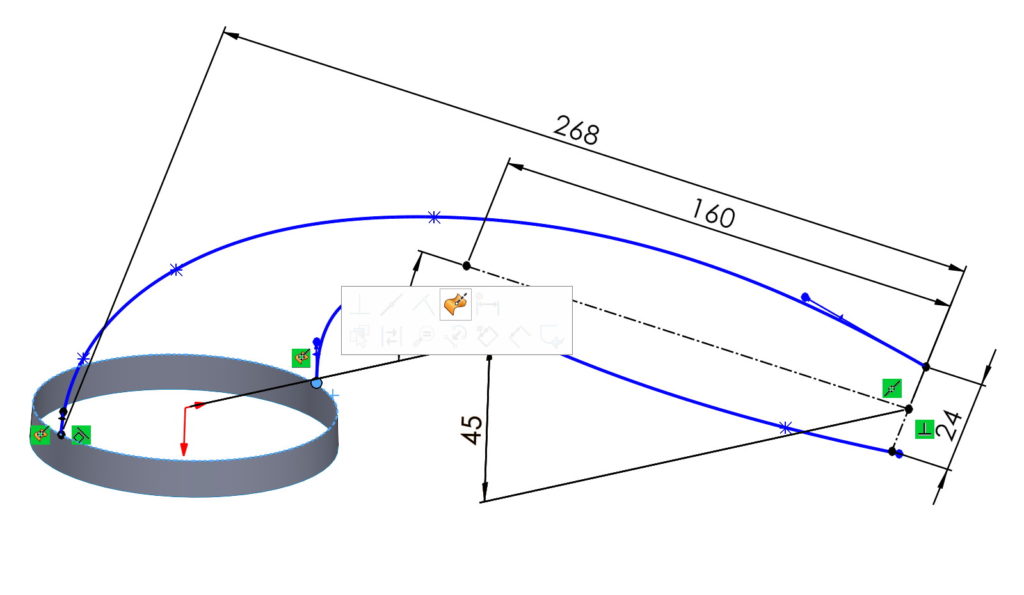
原來係咁, że chcąc odpowiednio powiązać szkic płaski znajdujący się na innej płaszczyźnie, nie wystarczy użyć 常見. Należy wybrać relację 穿刺, która jest “mocniejsza”, ale przede wszystkim pozwala całkowicie zdefiniować szkic.
Żeby opisać relację Przebicia możemy sobie wyobrazić nieskończenie wielką płaszczyznę i przewód/pręt, który w którymś miejscu ją przecina. Ten punkt stanowi właśnie 穿刺.
W praktyce sprowadza się to do tego, że szkic na płaszczyźnie prostopadłej do krawędzi musi być z nią powiązany przebiciem. Takie punkty przebicia znajdują się dwa, ale program powiąże szkic w bliższym zaznaczenia punkcie.
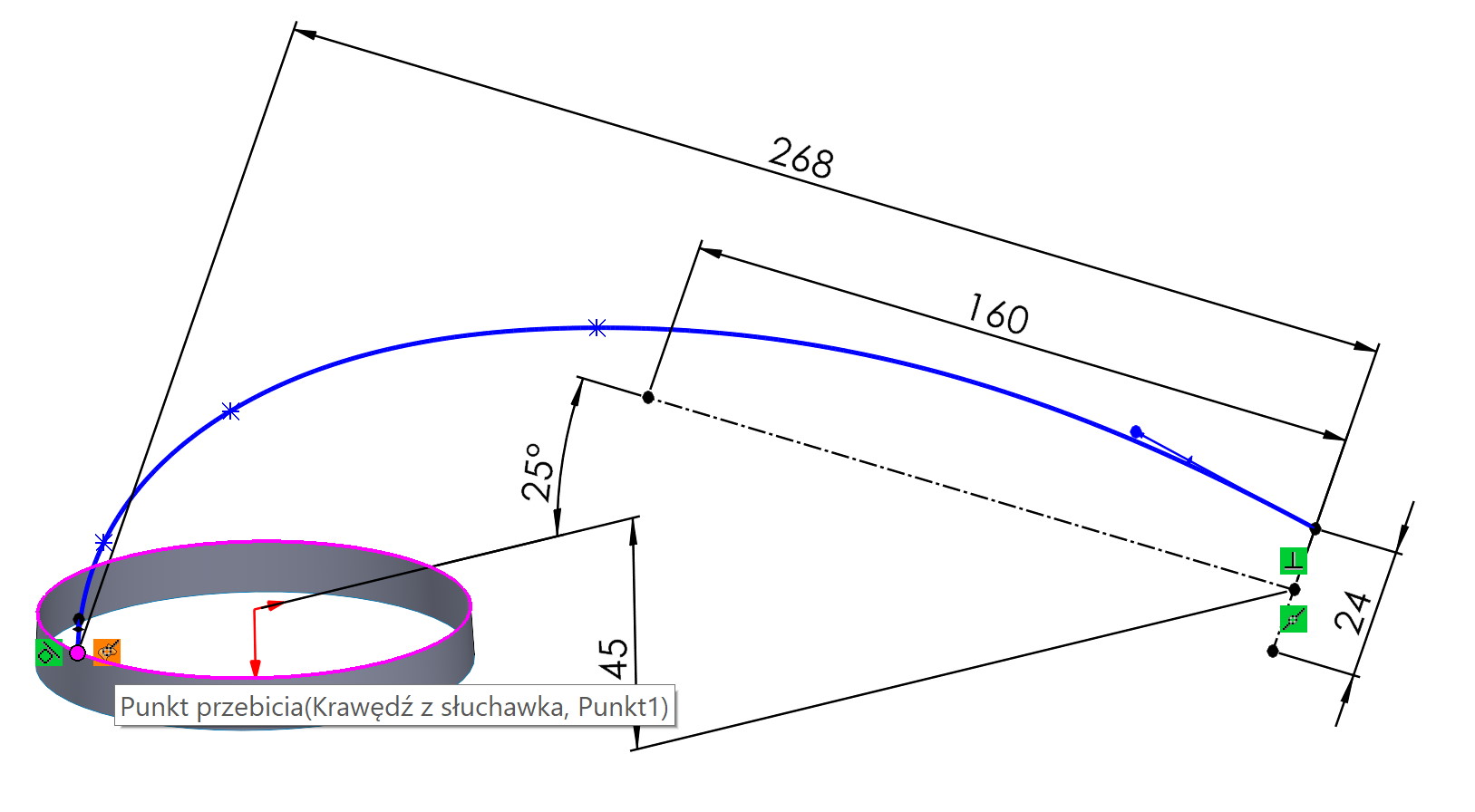
Gdyby zamiast Przebicia zastosować w takim miejscu relację 常見 – to punkt końcowy szkicu mógłby się swobodnie przesuwać wzdłuż krawędzi.
另一個例子.
Szkic profilu otrzymał relację 穿刺 ze ścieżką, którą stanowi Helisa o zmiennym skoku. 注意, że takich punktów przebicia w tym przykładzie może być wiele, program jednak przebija w najbliższym punkcie.
Co by się stało, gdyby zamiast Przebicia użyć 常見? Otóż ten sam punkt szkicu mógłby się swobodnie przemieszczać wzdłuż krzywej, która z punktu widzenia szkicu stanowi płaską “sinusoidę”. Oczywiście tym samym szkic staje się 未定義, więc takie rozwiązanie nie jest poprawne.